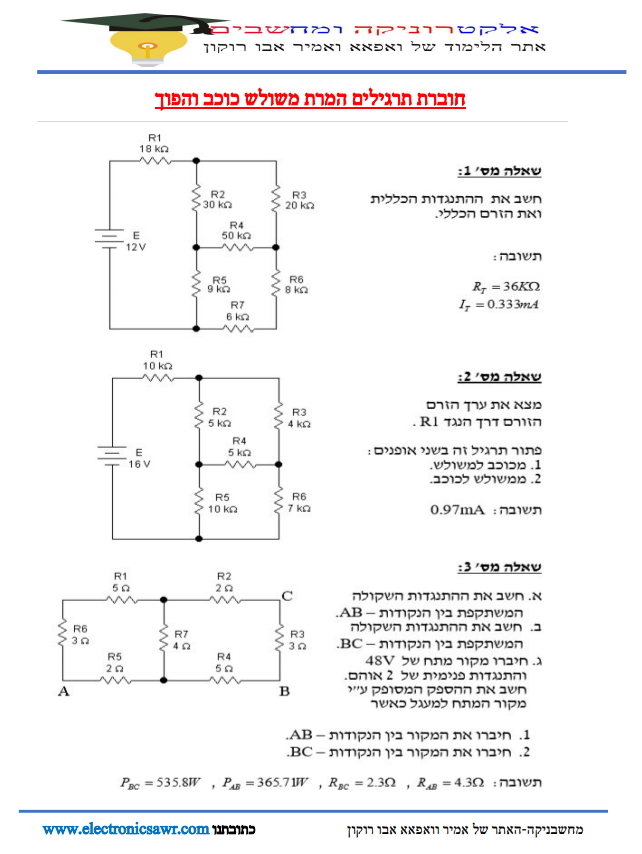
שער AND “וגם”

בואו ניקח דוגמה

אני אלך לשחק כדורגל היום אם אקבל את החולצה שהזמנתי וגם אקבל כדור חדש

אנחנו מזהים פה שני תנאים

הראשון אקבל את החולצה שהזמנתי-בואו נסמנו באות x.

השני-אקבל כדור חדש-בואו נסמנן באות y.

את התנאי AND (גם) מסמנים בסימן ∧

עכשיו לפי המשפט שבדוגמה בשפה המילולית בשביל שאני אלך לשחק כדורגל צריך שיתקיימו שני התנאים ביחד, מספיק שאחד מהם לא יתקיים ואני לא אלך לשחק כדורגל היום.

בואו נסכים שאם תנאי מתקיים נסמן את התוצאה1

ואם תנאי לא מתקיים נסמן את התוצאה ב0.

עכשיו נערוך טבלה ונרשום בה כל התנאים האפשריים ואת התוצאה, ונבטא אותם בעזרת x,y  ותוצאת

והנה עתה ערכנו את טבלת האמת הראשונה שלנו לביטוי בוליאני.

לחדי עיין ביניכם ישר ישימו לב שפעולת AND באלגברה בוליאנית אפשר לבטא בסימן המתמטי כפל(*)

בואו נוכיח זאת ונקח את הערכים מהטבלה

0*0=0

0*1=0

1*0=0

1*1=1

אם לא הבחנתם בזה בואו תסתכלו על השוואה בין 2 הטבלאות(טבלה אחת מתארת את פעולת הכפל וטבלה שנייה מתארת את AND

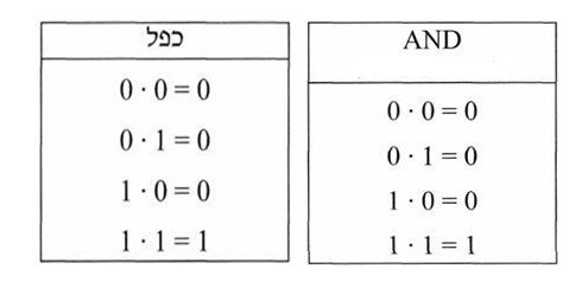
אתם שמים לב שהטבלאות זהות

מה שעתה מימשנו הוא הביטוי AND

יש לנו באלגברה הבוליאנית שער שנקרא AND ומציירים אותו

באחת מהצורות הבאות

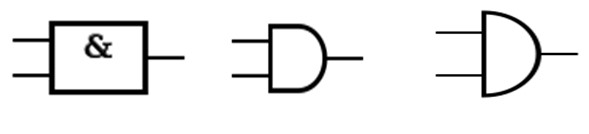
אם אנחנו רוצים לדמות את מצב AND לעולם החשמל נא להסתכל באיור הבא

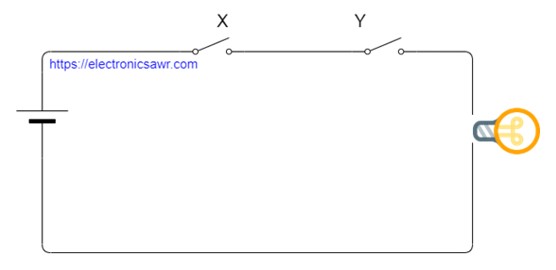
מפסק סגור מדמה 1

מפסק פתוח מדמה 0

אם אתם שמים לב המנורה תידלק רק כששני המפסקים סגורים

בכל מצב אחר המנורה לא תידלק