מספרים מורכבים
ספריית הקריאה
מספרים מורכבים
מספרים מורכבים
1. היכרות עם מספרים מרוכבים
בדף זה נלמד ונתרגל חיבור, חיסור וכפל של מספרים מרוכבים.
הקדמה:
מספר מרוכב הוא מהצורה : z = a + bi , כאשר:
a (האיבר החופשי – שלא נכפל ב – i ) נקרא החלק הממשי , מסומן ב- (Re(z.
b*i נקרא החלק המדומה , מסומן ב – (Im(z.
a ו – b הם מספריים ממשיים.
המספר מוגדר כמרוכב בגלל המכפלה במספר ‘ i ‘ .
המספר i הוא השורש הריבועי של 1- .
כלומר : i 2 = -1 .
עוד הגדרות:
– מספר אשר אינו נכפל ב – i , נקרא “ממשי טהור” – מורכב רק מחלק ממשי.
– מספר אשר כולו מכפלה של i , נקרא “מדומה טהור” – מורכב רק מחלק מדומה.
דוגמאות:
– z = 2 + 3i הוא מספר מרוכב , כאשר “2” הוא החלק הממשי שלו , ו- “3i” החלק המדומה.
– z = 5 הוא מספר ממשי טהור , מכיוון שאין בו כפולה של i. ניתן לומר שהחלק המדומה הוא 0.
– z = i הוא מספר מדומה טהור , מכיוון שאין בו חלק ממשי (שאינו נכפל ב i). ניתן לומר שהחלק הממשי הוא 0.
2. חיבור מספרים מרוכבים
כאשר אנו מחברים מספרים מרוכבים , החיבור יתבצע בנפרד עבור החלק הממשי , ועבור החלק המדומה.
-עבור החלק הממשי פשוט נחבר את שני המספרים הממשיים.
-עבור החלק המדומה , נוציא גורם משותף i , וישארו לנו שני מספרים ממשיים – אותם נוכל לחבר כרגיל.
לדוגמה:
-יהיו שני מספרים מרוכבים:
z1 = a + bi
z2 = c + di
-אזי הסכום שלהם הוא:
= z1 + z2 = a + bi + c + di
(a + c) + i*(b + d) =
תרגילים
חברו את המספרים המרוכבים הבאים:
תרגיל 1
z1 = 2 + 3i
z2 = 4 + i
פתרון
בחיבור מספרים מרוכבים, נחבר בנפרד את החלקים הממשיים ואת החלקים המדומים.
עבור החלקים המדומים נוציא גורם משותף i .
(z1 + z2 = 2 + 3i + 4 + i = (2+4) + i*(3+1
תשובה:
z1 + z2 = 6 + 4i
תרגיל 2
z1 = 1 + 2i
z2 = 3 – 4i
פתרון
בחיבור מספרים מרוכבים, נחבר בנפרד את החלקים הממשיים ואת החלקים המדומים.
עבור החלקים המדומים נוציא גורם משותף i .
(z1 + z2 = 1 + 2i + (3 – 4i) = (1 + 3) + i*(2 – 4
תשובה:
z1 + z2 = 4 – 2i
תרגיל 3
z1 = -2i
z2 = 5 + 6i
פתרון
נשים לב כי z1 הוא מדומה טהור, לכן החלק הממשי שלו הוא 0.
(z1 + z2 = 0 – 2i + (5 + 6i) = (0 + 5) + i*(-2 + 6
תשובה:
z1 + z2 = 5 + 4i
תרגיל 4
z1 = 3 – i
z2 = 4
פתרון
נשים לב כי z2 הוא ממשי טהור, לכן החלק המדומה שלו הוא 0.
(z1 + z2 = 3 – i + 4 = (3 + 4) + i*(-1 + 0
תשובה:
z1 + z2 = 7 – i
3. חיסור מספרים מרוכבים
חיסור מספרים מרוכבים ייעשה בצורה דומה לחיבור , כפי שכבר ראינו.
-עבור החלק הממשי נחסר את שני המספרים הממשיים.
-עבור החלק המדומה , נוציא גורם משותף i , וישארו לנו שני מספרים ממשיים – אותם נוכל לחסר כרגיל.
תרגילים
חסרו את המספרים המרוכבים הבאים:
תרגיל 1
z1 = 6 + 3i
z2 = 3 + 2i
פתרון
בחיסור מספרים מרוכבים, נחסר בנפרד את החלקים הממשיים ואת החלקים המדומים.
עבור החלקים המדומים נוציא גורם משותף i .
(z1 – z2 = 6 + 3i – (3 + 2i) = (6 – 3) + i*(3 – 2
תשובה:
z1 – z2 = 3 + i
תרגיל 2
z1 = 4 – 3i
z2 = 1 – 3i
פתרון
((z1 – z2 = 4 – 3i – (1 – 3i) = (4 – 1) + i*(-3 – (-3
תשובה:
z1 – z2 = 3
מסקנה – בחיבור / חיסור של 2 מספרים מרוכבים – יכול להתקבל מספר ממשי טהור.
תרגיל 3
z1 = 1 – i
z2 = 1 – 5i
פתרון
((z1 – z2 = 1 – i – (1 – 5i) = (1 – 1) + i*(-1 – (-5
תשובה:
z1 – z2 = 4i
מסקנה – בחיבור / חיסור של 2 מספרים מרוכבים – יכול להתקבל מספר מדומה טהור.
4. כפל של מספרים מרוכבים
כפל של מספרים מרוכבים דומה לכפל של מספרים ממשיים.
הכפל יתבצע באמצעות פתיחת סוגריים וכינוס איברים דומים.
חשוב לזכור: i2 = -1 .
לכן כאשר נכפול שני איברים מדומים – הם יהפכו למספר ממשי.
תרגילים
כפלו את המספרים המרוכבים הבאים:
תרגיל 1
z1 = 2 + 2i
z2 = 3 + i
פתרון
z1 * z2 = (2 + 2i) * (3 + i) = 2*3 + 2*i + 2i*3 + 2i*i
נזכור כי i2 = -1. לכן:
(z1 * z2 = 6 +2i + 6i +2*(-1
נותר לכנס איברים דומים.
תשובה:
z1 * z2 = 4 + 8i
תרגיל 2
z1 = 1 – i
z2 = -2 + 4i
פתרון
z1 * z2 = (1 – i) * (-2 + 4i) = 1*-2 + 1*4i + (-i)*(-2) + (-i)*4i
נזכור כי i2 = -1. לכן:
(z1 * z2 = -2 + 4i + 2i -4*(-1
נותר לכנס איברים דומים.
תשובה:
z1 * z2 = 2 + 6i
תרגיל 2
z1 = i
z2 = 4 – 5i
פתרון
(z1 * z2 = (i) * (4 – 5i) = 4*i + i*(-5i
נזכור כי i2 = -1. לכן:
(z1 * z2 = 4i – 5*(-1
נותר לכנס איברים דומים.
תשובה:
z1 * z2 = 5 + 4i
תרגיל 3
z1 = -3 – 2i
z2 = 4
פתרון
z1 * z2 = (-3 – 2i) * (4) = -3*4 -2i*4
המספר המרוכב z2 הוא ממשי טהור , לכן לא תהיה מכפלה של i בעצמו.
תשובה:
z1 * z2 = -12 – 8i
תרגיל 4
z1 = 2 + i
z2 = 2 – i
פתרון
(z1 * z2 = (2 + i) * (2 – i) = 2*2 – 2*i + 2*i + i*(-i
נזכור כי i2 = -1. לכן:
z1 * z2 = 4 – 2i + 2i + 1
נותר לכנס איברים דומים.
תשובה:
z1 * z2 = 5
מסקנה: במקרים מסוימים, מכפלת שני מספרים מרוכבים תהיה מספר ממשי
1. מציאת המספר הצמוד
המספר הצמוד:
הגדרה:
יהי מספר מרוכב z = a + bi
אזי , המספר הצמוד שלו הוא :![]()
המספר הצמוד מסומן בקו עליון , כפי שניתן לראות בנוסחה הנ”ל.
– החלק הממשי של המספר המרוכב והצמוד שלו זהה.
– החלק המרוכב של המספר המרוכב והצמוד שלו – זהה בגודל , הפוך בסימן.
תכונות חשובות:
1. הערך המוחלט של מספר מרוכב והצמוד שלו זהה.
2.כאשר נכפול מספר מרוכב בצמוד שלו , נקבל מספר ממשי.
המספר הממשי שקיבלנו הוא הריבוע של ערך המוחלט של המספר המרוכב.
כלומר:


:אם נשתמש בנוסחאות הכפל המקוצר, ניתן לפתור גם כך
![]()
לדוגמה:
z1 = 2 + 3i
z2 = 2 – 3i , הצמוד של z1.
z1 * z2 = (2 + 3i)*(2 – 3i) = 4 – 6i + 6i – 9i2
13 = 9 + 4 =
2|z1*z2 = 13 = |z1|2 = |z2
3. הסכום של מספר מרוכב והצמוד שלו – יהיה שווה לפעמיים החלק הממשי.
כלומר:![]()
4. חיסור בין מספר מרוכב והצמוד שלו – יהיה שווה לפעמיים החלק המדומה.
כלומר:![]()
תרגילים
מצאו את הצמוד של המספרים המרוכבים הבאים:
תרגיל 1
z = 2 + 5i
פתרון
החלק הממשי של הצמוד נשאר זהה.
החלק המדומה של הצמוד בעל סימן הפוך.
לכן:![]()
תרגיל 2
z = 3i
פתרון
המספר המרוכב הוא מדומה טהור.
לכן החלק הממשי שלו ושל הצמוד שלו הוא 0.
החלק המדומה של הצמוד שלו יהיה הפוך בסימן.
לכן:![]()
תרגיל 3
z = 4
פתרון
המספר בתרגיל זה הוא ממשי טהור.
לכן החלק המדומה שלו ושל הצמוד שלו הוא 0.
החלק הממשי שלו ושל הצמוד יהיה זהה.
לכן:![]()
כלומר , צמוד של מספר ממשי טהור הוא המספר עצמו , ללא שינוי.
תרגיל 4
z = 3 – 4i
מצאו את הערך המוחלט של z , בעזרת המכפלה שלו בצמוד. (ללא שימוש בנוסחה למציאת ערך מוחלט).
פתרון
לפי תכונות המספר הצמוד, מכפלת מספר מרוכב והצמוד שלו שווה לערך המוחלט.
לכן ראשית נמצא את המספר הצמוד, ולאחר מכן נכפול את שני המספרים.
תוצאת המכפלה תהיה הריבוע של הערך המוחלט.
לכן בשביל למצוא את הערך המוחלט ניקח את שורש המכפלה.
1. המספר הצמוד:![]()
2. מכפלת שני המספרים:![]()
![]()
נזכור כי i2 = -1![]()
תשובה: הערך המוחלט הוא השורש של מכפלת הצמודים.
כלומר : הערך המוחלט הוא 25√ = 5.
2. חילוק מספרים מרוכבים
בחילוק מספרים מרוכבים – מהצורה:
יש לנו בעיה מכיוון שהמכנה הוא מרוכב, ואנו לא יודעים לחלק במספר מרוכב.
לכן, בחילוק מספרים מרוכבים – נכפול את המונה ואת המכנה בצמוד של המכנה.
ראינו כי כאשר כופלים מספר בצמוד שלו מקבלים מספר ממשי.
לכן, יהיה לנו מספר ממשי במכנה, ונוכל לבצע את החילוק.
הערות:
1. חשוב לזכור כי כופלים את המונה בצמוד של המכנה , ולא בצמוד של המונה.
לאחר ההכפלה – יהיה לנו מספר ממשי במכנה , ונוכל לחלק כרגיל.
תרגילים:
מצאו את מנת המספרים המרוכבים הבאים:
(התשובה היא מספר מרוכב)
תרגיל 1
פתרון
- נכפול את המונה ואת המכנה בצמוד של המכנה.

(מכפלת מספר מרוכב בצמוד שלו שווה ל – a2 + b2. )
( i2 = -1 ) - נבצע חילוק בין המונה למכנה (בדומה למספרים ממשיים):
 לכן התשובה:
לכן התשובה:
תרגיל 2
פתרון
- נכפול את המונה והמכנה בצמוד של המכנה:

(מכפלת מספר מרוכב בצמוד שלו שווה ל – a2 + b2. )
( i2 = -1 )
- נבצע חילוק בין המונה למכנה (בדומה למספרים ממשיים):
 לכן התשובה:
לכן התשובה:
תרגיל 3
פתרון
- נכפול את המונה והמכנה בצמוד של המכנה:

(מכפלת מספר מרוכב בצמוד שלו שווה ל – a2 + b2. )
נחלק את המונה והמכנה ב – 8. נקבל:
- נבצע חילוק בין המונה למכנה (בדומה למספרים ממשיים):

לכן התשובה:
תרגיל 4 – העשרה – עם פרמטרים
נתונה המנה:
(כאשר a ו -b ממשיים , שונים מ – 0)
א. רשמו את תוצאת המנה כמספר מרוכב (באמצעות הפרמטרים a,b).
ב. נתון כי המנה שווה למספר המרוכב :
מצאו את ערכי הפרמטרים a ו -b.
פתרון
א. ביצוע החילוק:
1. נכפול את המונה והמכנה בצמוד של המכנה:
(מכפלת מספר מרוכב בצמוד שלו שווה ל – a2 + b2. )

2. נבצע חילוק בין המונה למכנה (בדומה למספרים ממשיים):
הביטוי הנ”ל הוא התשובה לסעיף א’.
(ניתן לראות כי מדובר במספר מרוכב , מכיוון שיש לו חלק מדומה וחלק ממשי.)
ב. מציאת הפרמטרים a ו -b :
נשתמש בנתון , ונשווה בין המספר המרוכב שמצאנו בסעיף א’ , לבין המספר המרוכב הנתון.
שני מספרים מרוכבים הם שווים , רק אם שני החלקים הממשיים זהים , ושני החלקים המדומים זהים.
לכן נקבל 2 משוואות:
1. שוויון החלק הממשי:
2.שוויון החלק המדומה:
פתרון מערכת המשוואות:
- נבצע כפל בהצלבה:
(a2 + b2 = 5*(2a – b - נבצע כפל בהצלבה:
(a2 + b2)*2 = 5*(a + 2b)
(a2 + b2 = (5/2) * (a + 2b
כעת נשווה בין הביטויים שקיבלנו עבור a2 + b2 :
(2a – b)*5 = (5/2) * (a + 2b)
נכפול את שני האגפים ב: 2/5
4a – 2b = a + 2b
3a = 4b
b = 3a/4
נציב את ערך ה- b שמצאנו כעת, במשוואה הראשונה.
(a2 + (3a/4)2 = 5*(2a – 3a/4
(a2 + 9a2/16 = 5*(5a/4
נכפול את המשוואה ב – 16:
16a2 + 9a2 = 16*5*5a/4
25a2 = 100a
נחלק ב – a (נתון כי שונה מ -0):
25a = 100
a = 4
על מנת למצוא את b, נציב a = 4 במשוואה : b = 3a/4.
לכן: b = 3*4/4
b = 3
לכן , המנה הראשונית הייתה:
הצגה טריגונומטרית של מספרים מרוכבים
הקדמה:
למספרים מרוכבים ישנן שתי צורות רישום:
1. הצגה אלגברית – ההצגה “הרגילה”, למשל : z = 2 + 3i
2. ההצגה הטריגונומטרית – נקראת גם בשם “הצגה במישור גאוס” – שהוא מישור המספרים המרוכבים.
נקראת גם “הצגה קוטבית” , או “הצגה פולארית”.
בדף זה נלמד מהי ההצגה הטריגונומטרית, ונלמד לעבור בין שתי צורות הרישום.
- נושאים נוספים בהקשר של מספרים מרוכבים נמצאים בקישור.
מישור גאוס – מישור המספרים המרוכבים
לפני שנלמד על ההצגה הטריגונומטרית, נכיר מעט את מישור גאוס.
מישור גאוס , או מישור המספרים המרוכבים , מאפשר לנו לראות את המספרים המרוכבים בצורה גאומטרית.
בדומה למישור xy, איתו אנו עובדים בפונקציות ממשיות, קיים המישור הזה, אשר מתאים למספרים מרוכבים.
הציר האופקי שלו הוא הציר הממשי (Re). (במקום ציר x)
הציר האנכי שלו הוא הציר המדומה (Im). (במקום ציר y)
ההצגה הטריגונומטרית:
כשמה כן היא, ההצגה הטריגונומטרית משתמשת בפונקציות הטריגונומטריות cos , sin ,
על מנת לייצג את המספרים המרוכבים.
היא נקראת גם הצגה פולרית / קוטבית , ויש לה שימוש בהרבה תחומים במתמטיקה.
צורתה של ההצגה הטריגונומטרית:
(z = r(cosθ + i sinθ
r – הרדיוס , מרחק הנקודה מהראשית. (הנקודה מייצגת את המספר המרוכב)
θ – הזווית אשר הנקודה נמצאת בה. (נמדדת מציר x – הציר הממשי).
r*cosθ – שיעור ה-x של המספר המרוכב – מסמל את החלק הממשי.
r*sinθ – שיעור ה-y של המספר המרוכב – מסמל את החלק המדומה – לכן נכפל ב – i.
*הערה: כאשר אנו מכפילים את הרדיוס ב – cosθ , נקבל את הצלע ליד הזווית – כלומר הצלע בציר הממשי.
כאשר אנו מכפילים את הרדיוס ב – sinθ , נקבל את הצלע מול הזווית – כלומר הצלע בציר המדומה.

עבור הדוגמה בגרף הנ”ל:
z = 1 + i – המספר המרוכב בצורתו האלגברית.
r = √2
θ = 45º
r*cosθ = 1
r*sinθ = 1
לכן המספר בצורתו הטריגונומטרית:
(z = √2 * (cos45 + i*sin45
**על מנת לקצר , לעיתים רושמים z = r * cisθ. זהו קיצור , בעל אותה משמעות כמו הביטוי הנ”ל.
cisθ = cosθ + i*sinθ
הקשר בין 2 שיטות הייצוג ומעבר ביניהן:
עבור כל הצגה, נצטרך למצוא שני פרמטרים:
– הצגה אלגברית – a ו – b
-הצגה טריגונומטרית – r ו – θ
א. מעבר מהצגה אלגברית לטריגונומטרית:
במעבר מסוג זה a,b יהיו נתונים.
ניתן לראות בגרף שלמעלה , כי הרדיוס הוא היתר במשולש ישר זווית , שבסיסיו הם a ו – b .
לכן את הרדיוס (r) נמצא על פי הנוסחה הזו:
![]()
ניתן לראות בגרף שלמעלה , כי: tanθ = b/a
לכן , את הזוויות θ נמצא על פי הנוסחה הזו:

ב. המעבר ההפוך – מהצגה טריגונומטרית לאלגברית:
הנוסחאות יהיו לפי טריגונומטרית פשוטה.
1. a = r*cosθ
2. b = r*sinθ
תרגילים
מעבר מהצגה אלגברית לטריגונומטרית
תרגיל 1
נתון המספר המרוכב z = 2 + 2i
רשמו את המספר בהצגה טריגונומטרית
פתרון
המספר המרוכב נתון בהצגה אלגברית. נרצה להעבירו להצגה טריגונומטרית.
לכן נרצה למצוא את הרדיוס (r) , ואת הזווית (θ).
נעבוד לפי נוסחאות המעבר מהצגה אלגברית לטריגונומטרית:
1.![]()
לכן:![]()
2.
לכן:
(θ = arctan(2/2) = arctan(1
θ = 45° או θ = 225.
(2 הזויות מקיימות את המשוואה).
נשים לב כי המספר המרוכב נמצא ברביע הראשון של מישור גאוס (a ו -b חיוביים).
לכן נבחר θ = 45°.
לכן התשובה:
(z = √8*(cos45 + i*sin45
או, בעזרת הקיצור :
z = √8 * cis 45

תרגיל 2
נתון המספר המרוכב z = 1 – √3i
רשמו את המספר בהצגה טריגונומטרית
פתרון
המספר המרוכב נתון בהצגה אלגברית. נרצה להעבירו להצגה טריגונומטרית.
לכן נרצה למצוא את הרדיוס (r) , ואת הזווית (θ).
נעבוד לפי נוסחאות המעבר מהצגה אלגברית לטריגונומטרית:
1.![]()
לכן:![]()
2.
לכן:
(θ = arctan(-√3 / 1) = arctan(-√3
θ = 120° או °θ = 300.
(2 הזויות מקיימות את המשוואה).
נשים לב כי המספר המרוכב נמצא ברביע הרביעי של מישור גאוס (a חיובי , b שלילי).
לכן נבחר θ = 300°.
לכן התשובה:
(z = 2*(cos300 + i*sin300
או, בעזרת הקיצור :
z = 2 * cis 300

תרגיל 3
נתון המספר המרוכב z = 4i
רשמו את המספר בהצגה טריגונומטרית
פתרון
נשים לב כי המספר הוא מדומה טהור. לכן a = 0.
המספר המרוכב נתון בהצגה אלגברית. נרצה להעבירו להצגה טריגונומטרית.
לכן נרצה למצוא את הרדיוס (r) , ואת הזווית (θ).
נעבוד לפי נוסחאות המעבר מהצגה אלגברית לטריגונומטרית:
1.![]()
לכן:![]()
2.
לכן:
לא מוגדר! = (θ = arctan(4 / 0
חילוק ב – 0 הוא לא מוגדר.
אבל אנו יודעים כי המספר הוא מדומה טהור , לכן בוודאות הוא נמצא על הציר המדומה (האנכי).
לכן הזווית היא θ = 90° או θ = 270°.
b של המספר הנתון הוא חיובי. לכן המספר נמצא בחלק החיובי של הציר המדומה.
לכן θ = 90°.
לכן התשובה:
(z = 4*(cos90 + i*sin90
או, בעזרת הקיצור :
z = 4 * cis 90

מעבר מהצגה טריגונומטרית לאלגברית:
תרגיל 4
נתון המספר המרוכב בהצגה טריגונומטרית:
(z = 4*(cos30 + i*sin30
רשמו את המספר בהצגה אלגברית
פתרון
עבור המספר הנתון : r = 4 , θ = 30°.
על מנת למצוא את המספר בהצגה אלגברית , נצטרך למצוא את a ו -b.
נמצא אותם לפי הנוסחאות:
1. a = r*cosθ
לכן : a = 4*cos(30) = 4*√3 /2
a = 2*√3
2. b = r*sinθ
לכן: b = 4*sin(30) = 4*0.5
b = 2
לכן התשובה:
z = 2√3 + 2i

תרגיל 5
נתון המספר המרוכב בהצגה טריגונומטרית:
(z = √2*(cos135 + i*sin135
רשמו את המספר בהצגה אלגברית
פתרון
עבור המספר הנתון : r = √2 , θ = 135°.
על מנת למצוא את המספר בהצגה אלגברית , נצטרך למצוא את a ו -b.
נמצא אותם לפי הנוסחאות:
1. a = r*cosθ
לכן : (a = √2*cos(135) = √2*(-√2 /2
a = -1
2. b = r*sinθ
לכן: (b = √2*sin(135) = √2*(√2 /2
b = 1
לכן התשובה:
z = -1 + i

תרגיל 6
נתון המספר המרוכב בהצגה טריגונומטרית:
(z = 3*(cos180 + i*sin180
רשמו את המספר בהצגה אלגברית
פתרון
עבור המספר הנתון : r = 3 , θ = 180°.
על מנת למצוא את המספר בהצגה אלגברית , נצטרך למצוא את a ו -b.
נמצא אותם לפי הנוסחאות:
1. a = r*cosθ
לכן : (a = 3*cos(180) = 3*(-1
a = -3
2. b = r*sinθ
לכן: b = 3*sin(180) = 3*0
b = 0
לכן התשובה:
z = -3
(קיבלנו מספר ממשי טהור) – הוא נמצא על הציר הממשי.

תרגיל מסכם:
מצאו את משוואת הישר המחבר בין הנקודות המיוצגות ע”י המספרים המרוכבים:
(z1 = (5*√2)*cis (45
(z2 = 10*cis (270
פתרון
1. נמצא את המספרים בהצגתם האלגברית – על מנת למצוא את שיעורי הנקודות.
א. z1:
(a = r*cosθ = (5*√2)*cos(45
(a = (5*√2) * (√2/2
a = 5
(b = r*sinθ = (5*√2)* sin(45
(b = (5*√2) * (√2/2
b = 5
לכן: z1 = 5 + 5i
לכן המספר המרוכב z1 מייצג את הנקודה:
(x1 , y1) = (a , b) = (5 , 5)
ב. z2:
(a = r*cosθ = 10*cos(270
a = 10*0
a = 0
(b = r*sinθ = 10* sin(270
(b = 10 * (-1
b = -10
לכן: z2 = -10i
לכן המספר המרוכב z2 מייצג את הנקודה:
(x2 , y2) = (a , b) = (0 , -10)
2. נמצא את משוואת הישר באמצעות 2 הנקודות שמצאנו:
א. שיפוע הישר:

ב. נקודה על הישר:
נבחר את הנקודה (10- , 0).
נוסחה למציאת משוואת המשיק : (y-y0 = m*(x-x0 , כאשר m הוא השיפוע, ו-(x0, y0) נקודת ההשקה.
נציב את הנתונים שמצאנו , ונקבל :
(y – (-10) = 3*(x – 0
y + 10 = 3x
y = 3x – 10

מספרים מרוכבים – חיבור וחיסור בהצגה טריגונומטרית
חיבור וחיסור בין מספרים מרוכבים כאשר נמצאים בהצגה טריגונומטרית – פעולה מסובכת.
לכן, כאשר נרצה לבצע חיבור וחיסור בין מספרים מרוכבים, קודם כל נעביר אותם להצגה אלגברית,
לאחר מכן נבצע את הפעולה הנדרשת.
לבסוף, אם נדרש מאיתנו, נחזיר את המספר המרוכב שמתקבל להצגה טריגונומטרית.
- נושאים נוספים בהקשר של מספרים מרוכבים תמצאו בקישור.
תרגילים:
תרגיל 1
(z1 = √2cis(45
(z2 = 4cis(120
חשבו את הסכום: z1 + z2.
(רשמו את התוצאה בהצגה אלגברית).
פתרון
על מנת לבצע את פעולת החיבור, ראשית נעביר את המספרים להצגה אלגברית:
z1:
a1 = √2 * cos(45) = 1
b1 = √2 * sin(45) = 1
z1 = 1 + i
z2:
a2 = 4 * cos(120) = -2
b2 = 4 * sin(120) = 2√3
z2 = -2 + 2√3*i
לכן הסכום:
(z1 + z2 = 1 + i + (-2 + 2√3 i
z1 + z2 = -1 + (2√3+1)*i
תרגיל 2
(z1 = 2cis(60
(z2 = 4cis(240
חשבו את ההפרש: z1 – z2.
(רשמו את התוצאה בהצגה טריגונומטרית).
פתרון
על מנת לבצע את פעולת החיסור, ראשית נעביר את המספרים להצגה אלגברית:
z1:
a1 = 2 * cos(60) = 1
b1 = 2 * sin(60) = √3
z1 = 1 + √3*i
z2:
a2 = 4 * cos(240) = -2
b2 = 4 * sin(240) = -2√3
z2 = -2 – 2√3*i
לכן ההפרש:
(z1 – z2 = 1 + √3*i – (-2 – 2√3 i
z1 – z2 = 3 + 3√3*i
תשובה בהצגה טריגונומטרית: (כנדרש בשאלה)
r = √[32 + (3√3)2] = 6
θ = arctan(3√3 / 3) = 60º
(z1 – z2 = 6cis(60
תרגיל 3
(z1 = 2cis(90
(z2 = 2cis(180
(z3 = √2*cis(135
חשבו את תוצאת הביטוי: z1 + z2 – z3
רשמו את התשובה בהצגה טריגונומטרית.
פתרון
על מנת לבצע את הפעולות, ראשית נעביר את המספרים להצגה אלגברית:
z1:
a1 = 2 * cos(90) = 0
b1 = 2 * sin(90) = 2
z1 = 2i
z2:
a2 = 2 * cos(180) = -2
b2 = 2 * sin(180) = 0
z2 = -2
z3:
a3 = √2 * cos(135) = -1
b3 = √2 * sin(135) = 1
z3 = -1 + i
לכן הביטוי:
(z1 + z2 – z3 = 2i – 2 – (-1 + i
z1 + z2 – z3 = -1 + i
תשובה בהצגה טריגונומטרית: (כנדרש בשאלה)
r = √(12 + 12) = √2
θ = arctan(1/-1) = 135º
(z1 + z2 – z3 = √2*cis(135
תרגיל 4
(z1 = √18 * cis(315
(z2 = 2cis(150
(z3 = 5cis(270
חשבו את תוצאת הביטוי: z1 – z2 – z3
רשמו את התשובה בהצגה אלגברית.
פתרון
על מנת לבצע את הפעולות, ראשית נעביר את המספרים להצגה אלגברית:
z1:
a1 = √18 * cos(315) = 3
b1 = √18 * sin(315) = -3
z1 = 3 – 3i
z2:
a2 = 2 * cos(150) = -√3
b2 = 2 * sin(150) = 1
z2 = -√3 + i
z3:
a3 = 5 * cos(270) = 0
b3 = 5 * sin(270) = -5
z3 = -5i
לכן הביטוי:
(z1 – z2 – z3 = 3 – 3i – (-√3 + i) – (-5i
z1 – z2 – z3 = 3 + √3 – 3i – i + 5i
z1 – z2 – z3 = (3 +√3) + i
כפל וחילוק מספרים מרוכבים בהצגה טריגונומטרית
עולות הכפל והחילוק הרבה יותר קלות לביצוע כאשר אנו בהצגה טריגונומטרית.
לכן כאשר אנו נדרשים לבצע כפל או חילוק של שני מספרים מרוכבים , נעדיף קודם להעבירם להצגה טריגונומטרית.
יהיו שני מספרים מרוכבים:
(z1 = r1 * cis(θ1
(z2 = r2 * cis(θ2
כפל:![]()
חילוק:
- דף זה הוא הפרק השביעי בנושא מספרים מרוכבים, פרקים נוספים תמצאו בקישור.
תרגילים
כפל:
חשבו את המכפלה של המספרים המרוכבים הבאים:
תרגיל 1
(z1 = 2 * cis(60
(z2 = 4 * cis(30
פתרון
נשתמש בנוסחה לכפל בהצגה טריגונומטרית:![]()
לכן:
(z1*z2 = 2*4 * cis(30 + 60
תשובה: (z1 * z2 = 8 * cis(90
תרגיל 2
(z1 = 0.5* cis(125
(z2 = 6 * cis(10
פתרון
נשתמש בנוסחה לכפל בהצגה טריגונומטרית:![]()
לכן:
(z1*z2 = 0.5*6 * cis(125 + 10
תשובה: (z1 * z2 = 3 * cis(135
חילוק:
חשבו את המנה של המספרים המרוכבים הבאים:
תרגיל 1
(z1 = 5* cis(180
(z2 = cis(60
פתרון
נשתמש בנוסחה לחילוק בהצגה טריגונומטרית:
לכן:
תשובה:![]()
תרגיל 2
(z1 = 6*cis(30
(z2 = 3*cis(120
פתרון
נשתמש בנוסחה לחילוק בהצגה טריגונומטרית:
לכן:![]()
![]()
זווית שלילית היא זווית הנמדדת בכיוון ההפוך – כלומר עם כיוון השעון.
לכן כדי להפוך אותה לזווית חיובית נחבר לה 360º , כלומר רק נוסיף עוד סיבוב שלם.
לכן זו תהיה אותה זווית , רק חיובית.
הזווית היא :
θ = -90 + 360 = 270º
תשובה:![]()
תרגילים נוספים:
תרגיל 1
z1 = 4i
z2 = -2 – 2i
z3 = 1 – √3i
חשבו את תוצאת הביטוי: 
פתרון
ראשית, כאשר מדובר בכפל וחילוק, נעדיף להעביר את המספרים להצגה טריגונומטרית:
(z1 = 4*cis(90
(z2 = √8 * cis(225
(z3 = 2 * cis(300
נשתמש בנוסחאות לכפל וחילוק בהצגה טריגונומטרית.
לכן:

תרגיל 2
z1 = -2 + 2√3*i
z2 = -8i
z3 = 1 + √3i
חשבו את תוצאת הביטוי: 
פתרון
ראשית, כאשר מדובר בכפל וחילוק, נעדיף להעביר את המספרים להצגה טריגונומטרית:
(z1 = 4*cis(120
(z2 = 8 * cis(270
(z3 = 2 * cis(60
נשתמש בנוסחאות לכפל וחילוק בהצגה טריגונומטרית.
לכן:
![]()
![]()
(נזכיר כי כאשר מקבלים זווית שלילית, מוסיפים לה 360 מעלות – על מנת לקבל זווית חיובית).
תרגיל 3
נתונה המשוואה:
מצאו את הפרמטר a.
פתרון
מטרתנו היא להגיע למשוואה פשוטה יותר – כדי להצליח למצוא את ערכו של a.
לכן:
בצד שמאל – נבצע את החילוק.
בצד ימין – נעביר לצורה טריגונומטרית.
נקבל:![]()
המספרים המרוכבים הנ”ל שווים , רק אם הזוית שלהם שווה.
לכן:
30a – 60 = 240
30a = 300
a = 10
חומרי עיון נוספים
קבצים שהורדנו מהאינטרנט כפי שהם
איזור הוידיאו והסרטונים
סרטונים נוספים בנושא מהרשת
איזור התרגילים
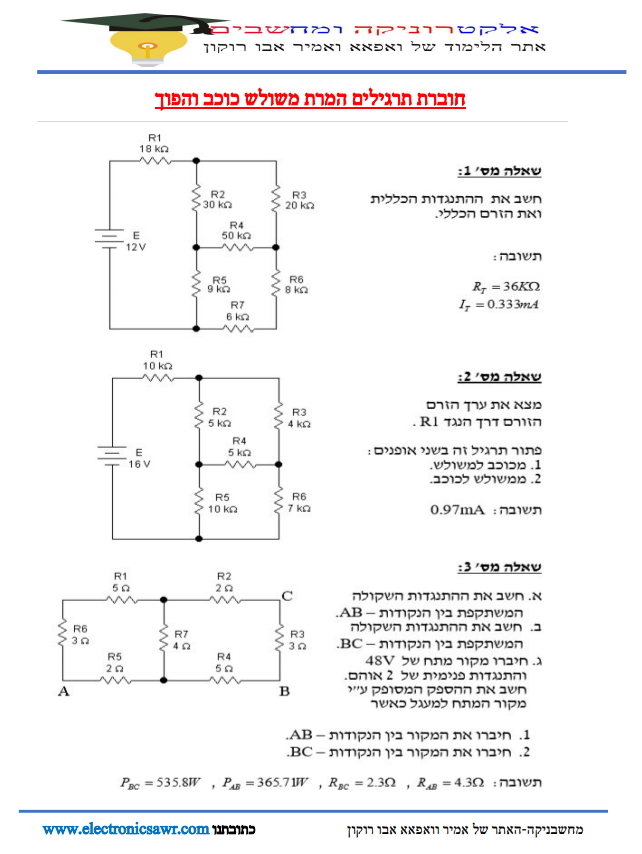
המרת כוכב משולש
- Ameer
- 22 פברואר 2021








