משפט ההרכבה (סופרפוזיציה) (The superposition theorem)

• יש רשתות חשמליות שבהן מחוברים כמה מקורות אנרגיה. אם מקורות האנרגיה ניתנים לצמצום ביניהם (כדוגמת חיבור טורי או אנטי טורי של מקורות מתח), דרך הפתרון זהה לרשתות שפתרנו עד כה. אך מה אפשר לעשות כשמקורות האנרגיה אינם ניתנים לצמצום (כדוגמת כמה מקורות אנרגיה ביותר מענף אחד במעגל)?

   

  במקרים אלה עלינו להיעזר במשפטי רשת או בשיטות לפתרון מעגלים. משפט ההרכבה (סופר-פוזיציה) משתייך לקבוצת משפטי הרשת והוא מסייע בפתרון של רשתות הכוללות כמה מקורות אנרגיה.

  חשוב לציין שמשפט זה תקף רק בעבור רשתות לינאריות, כלומר רשתות הכוללות רכיבים לינאריים בלבד כדוגמת נגדים, מקורות מתח ומקורות זרם.

   

  על פי משפט ההרכבה, מותר לחשב את  התרומה של כל אחד ממקורות האנרגיה, בנפרד, למתח או הזרם של אחד הנגדים במעגל ואחר כך לסכם את כל התרומות כדי לדעת מה המתח או הזרם באותו הנגד. שלבי הפתרון בשיטה זו תלויים במספר מקורות האנרגיה שיש במעגל. ככל שיהיו יותר מקורות אנרגיה במעגל, כן נשתמש פחות (מטעמי נוחות בלבד) במשפט זה. משפט ההרכבה מתבסס רובו על פתרון של מעגלים מעורבים עם מקור אנרגיה יחיד, ולכן הוא נחשב לשיטת פתרון פשוטה.

  לסיכום, יש לבצע הרכבה בין התוצאות שהתקבלו על ידי כל מקור בנפרד, הרכבה זו תתבצע על פי המפורט בשלבי הפתרון.

  שלבי הפתרון במשפט ההרכבה

  
  מספר שלבי הפתרון תלוי כאמור במספר מקורות האנרגיה במעגל. סך כל שלבי הפתרון המרבי, הוא כמספר מקורות האנרגיה במעגל ועוד אחד. בשימוש במשפט ההרכבה בפתרון רשתות יש לפעול על פי השלבים האלה:

  א.    בדיקת צמצום מקורות האנרגיה, כאלה שמחוברים באותו ענף. אי צמצום יגרום להארכת פתרון התרגיל, הואיל ומספר שלבי הפתרון תלוי במספר מקורות האנרגיה שקיימים במעגל.

  ב.     מציאת זרם דרך כל נגד וכיוון בכל אחד מן המעגלים שנוצרים כתוצאה מהשארת מקור אנרגיה יחיד ושיתוק כל שאר המקורות. שיתוק מקורות האנרגיה משמעו: קיצור מקורות מתח יש לקצר ואילו וניתוק מקורות זרם.

  ג.      מציאת הזרמים האמיתיים במעגל המקורי על ידי ביצוע הרכבה בין התוצאות שהתקבלו בסעיף (ב). ההרכבה היא בעצם הסכום האלגברי של הזרמים או המתחים לכל אחד מן הנגדים. זרמים, או מתחים, באותו כיוון יש לחבר, ואילו בכיוונים הפוכים יש לחסר (גדול פחות קטן). הכיוון שיקבע במקרה זה הוא כיוון הזרם, או המתח, הגדול.

  ד.    סרטוט המעגל המקורי עם הזרמים, או המתחים, האמיתיים וכיווניהם.

  תרגול חלק א

   

  • רגיל דוגמה

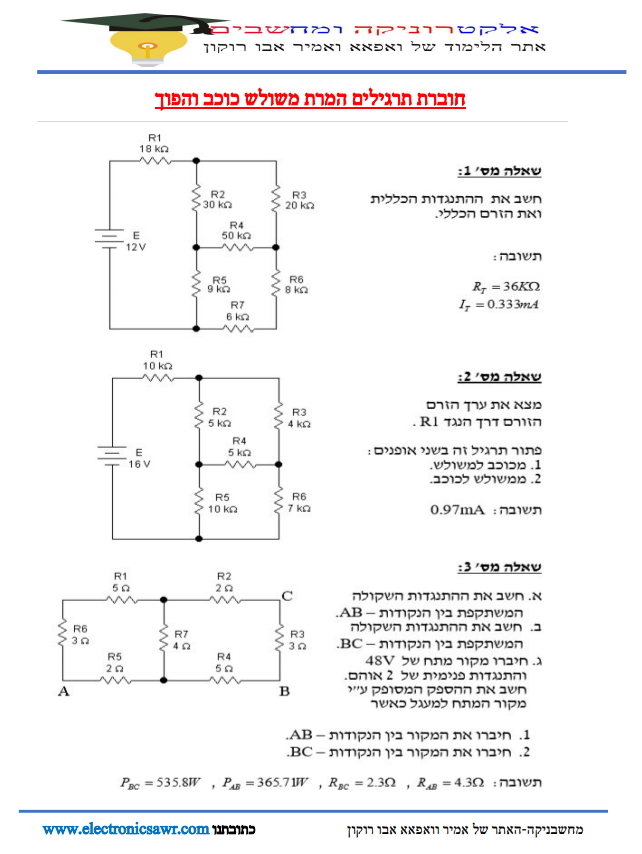
    נתון המעגל

    

    חשבו את:

    א.  עצמת הזרם וכיוונו דרך כל נגד;

    ב.     הספק בנגד R3 ;

    ג.      פוטנציאל בנקודה X .

     

    פתרון תרגיל דוגמה 

    ברשת הנתונה יש שני מקורות אנרגיה שלא ניתן לצמצם אותם, כלומר אנו לא יכולים לפתור את הרשת בדרך הרגילה כפי שפתרנו עד כה. נשתמש במשפט ההרכבה לצורך פתרון הרשת.

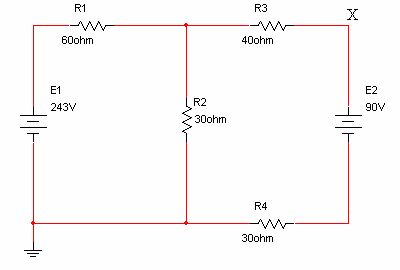
    1.   מציאת זרמים במעגל עבור מקור המתח E1

    

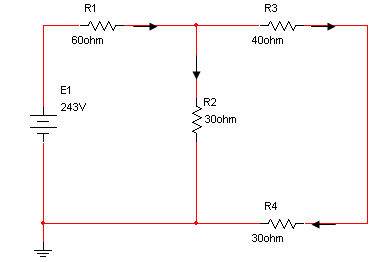
    נחשב זרם דרך כל נגד במעגל:

         

    

    מומלץ מאוד לציין את הזרמים שחושבו על גבי המעגל 

    

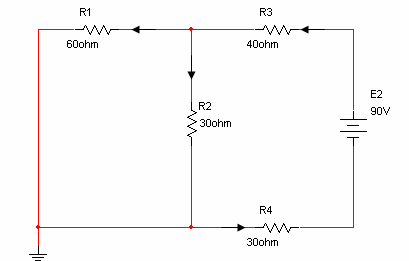
    מציאת זרמים במעגל בעבור מקור המתח E2

     

    • בשלב זה יש להשאיר את מקור המתח E2 ולשתק את שאר המקורות (E1). במעגל שהתקבל יש לקבוע את כיווני הזרמים דרך כל נגד ולחשב את עצמת הזרם דרכם.

      

    נחשב זרם דרך כל נגד במעגל:

    

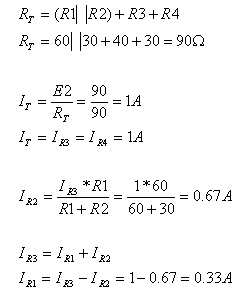
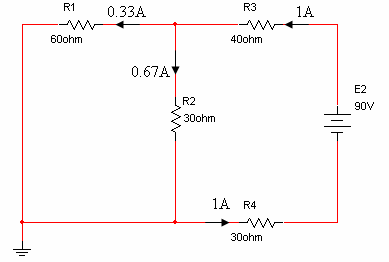
    מומלץ מאוד לציין את הזרמים שחושבו על גבי המעגל 

    

    מציאת זרמים במעגל המקורי – שלב ההרכבה

     

    •  

      בשלב זה יש לבצע הרכבה בין התוצאות שהתקבלו לשם מציאת הזרמים האמיתיים במעגל המקורי. לשם כך נתבונן בשני המעגלים הפתורים:

      

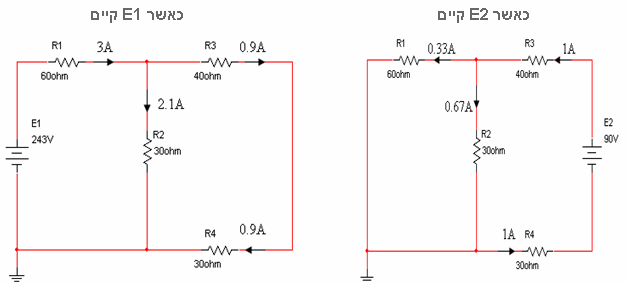
      חישוב הזרמים האמיתיים על ידי חיבור אלגברי של זרמי הנגדים – באותו כיוון מחברים, כיוונים הפוכים מחסרים (גדול פחות קטן):

       

       

      אפשר לקבוע את כיווני החיצים

      

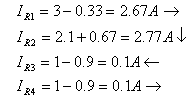
      נסמן זרמים אמיתיים אלה על המעגל המקורי שבאיור 

      

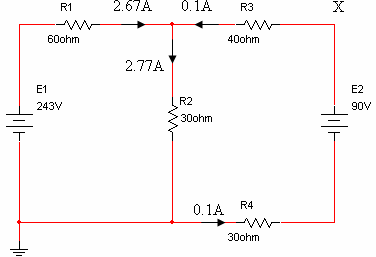
      לפני ביצוע סעיפי השאלה, אפשר לבדוק על פי חוק הזרמים של קירכהוף שאכן אין סתירה בתוצאות שהתקבלו:

      

      א.   זרם דרך כל נגד וכיוון מופיע גם על המעגל המקורי וגם בשלב ההרכבה.

       

      ב.   חישוב הספק בנגד R3:

      

      ג.   פוטנציאל המתח בנקודה X הוא ביחס לאדמה. לכן נבחר מסלול לאיסוף מתחים מנקודה X לאדמה: