מקרה כללי:

הזרם, המתח והמטען של פני הקבל כתלות בזמן t כאשר הפרמטרים ההתחלתיים הם: QC (0) , IC (0), UC (0) והפרמטרים במצב המתמיד הם:

QC (∞) , IC (∞), UC (∞) , מתנהגים בצורה הבאה:

מקרה פרטי- משוואה של מעגל טעינה:

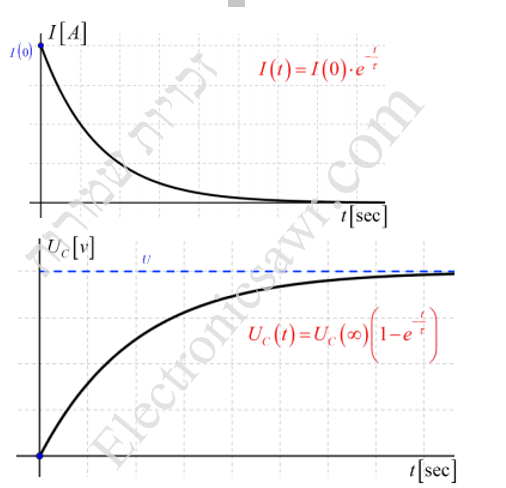
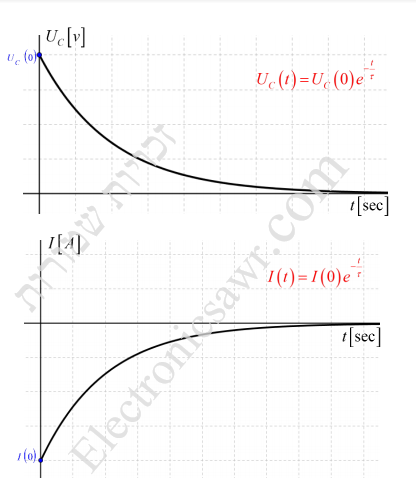
משוואת הדפקים נותנת לנו את האפשרות לחשב את מתח הקבל בכל רגע ורגע , מרגע סגירת המפסק ועד סיום טעינתו. לצורך זה יהיה עלינו להיעזר בחוק המתחים של קירכהוף:

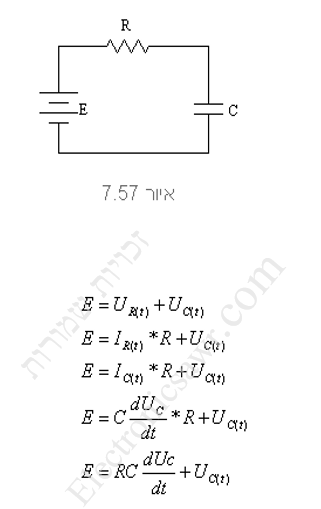
המשוואה שהתקבלה נקראת משוואה דיפרנציאלית מסדר ראשון עם מקדמים קבועים, זוהי משוואה הכוללת את הפןנקציה Uc את הנגזרת של אותה פונקציה dUc/dt. הפתרון של משוואה דיפרנציאלית נותן משפחה של פונקציות. כדי לדעת מהי הפונקציה המתאימה למקרה שלנו, עלינו ךדעת גם את תנאי התחלה. זהו המתח על הקבל ברגע t=0+ כלומר רגע קטן מאוד אחרי תחילת הטעינה. הפתרון שנקבל לבסוף יהיה Uc כתלות בזמן t. בעזרת פונרציה זאת נדע מהו המתח על הקבל בכל רגע נתון.

הפתרון של המשוואה הדיפרנציאלית המתקבל בעבור תנאי התחלה אפס הוא:

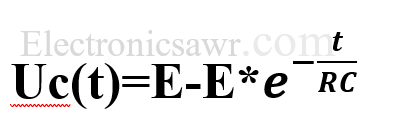
באמצעות המשוואה הזאת אפשר לחשב את המתח על הקבל בכל רגע נתון.

הפתרון הזה נכון רק אם תנאי ההתחלה הוא אפס.

הפתרון היותר כללי המתקבל בעבור תנאי התחלה שונה מאפס ידוע בשם משוואת הדפקים היסודית. השימושית בעבור פונקציות מעריכיות כמו השתנות המתח על הקבל הנטען ממקור מתח קבוע:

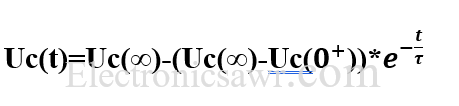
הערה:משוואה זו תקפה גם עבור זרם דרך הקבל במעגל RC עם מקור מתח קבוע.